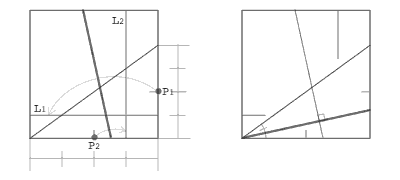
We usually use a straight edge and a compass for mathematical constructions. The straight-edge-and-compass construction is a finite sequence of the following three procedures on a plane with some points placed arbitrarily.
1. Given two points P1 and P2, to draw a line passing through both P1 and P2.
2. Given one point O and one segment P1P2, to draw a circle whose center is O and whose radius is the length of P1P2.
3. Given some lines and circles, to locate points of intersection.
We can also construct some lines and points with origami. We use folds in the origami construction, of course. But what kind of folds? We have many kinds of them, and not all are appropriate for constructions.
I will exclude curved folds, because we do not know about them very much. I will also avoid folding along plural straight lines at a time. Otherwise, it gets too complicated. Moreover, let's avoid using any tool such as a ruler, another sheet of paper, or even a pencil.
Under these conditions, we cannot place a point on the plane directly. If we make a fold arbitrarily, we get a line, not a point. To locate a point, we need at least two creases. In other words, any point in the origami construction has at least two lines passing through it.
Then, the origami construction would be a finite sequence of either "to fold a line at a time without any tool" or "given some creases, to locate points of intersection" on a plane with some lines placed arbitrarily.
Humiaki Huzita listed six folds which we can use in the origami construction.
A. Given two lines L1 and L2, to fold a line placing L1 onto L2.
B. Given two points P1 and P2, to fold a line placing P1 onto P2.
C. Given two points P1 and P2, to fold a line passing through both P1 and P2.
D. Given one point P and one line L, to fold a line passing through P and perpendicular to L.
E. Given two point P1 and P2 and one line L, to fold a line placing P1 onto L and passing through P2.
F. Given two point P1 and P2 and two lines L1 and L2, to fold a line placing P1 onto L1 and placing P2 onto L2.
I found another.
G. Given one point P and two lines L1 and L2, to fold a line placing P onto L1 and perpendicular to L2.
Robert Lang proved that these seven folds are complete. That is, there is no other fold in origami construction. We do not need more than seven folds to execute all possible construction. Then, do we need all seven of them? I will argue that we need only one fold, instead of seven.
First, we can consider the fold A to be the fold F with P1 being on L2 and P2 being on L1. When there are two lines L1 and L2, we can construct, using an arbitrary line, two points P2 and P1 on L1 and L2, respectively.
Second, we can also consider the fold B to be the fold F with P1 being on L2 and P2 being on L1. In the origami construction, there are always two lines L1 which passes through P2 but does not pass through P1 and L2 which passes through P1 but does not pass through P2 when there are two points P1 and P2.

Now let's look at the fold F. It is known that the crease is a common tangent of two parabolas p1 whose focus is P1 and whose directrix is L1 and p2 whose focus is P2 and whose directrix is L2. What happens if P2 comes close to L2?
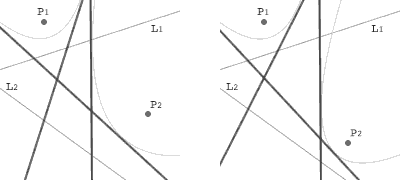
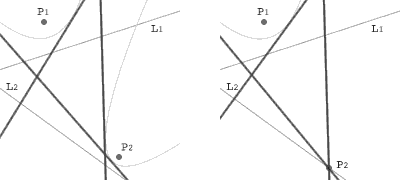
Set a Cartesian coordinate system so that P2 is on the x-axis and L2 equals the y-axis. Let the equation of L1 be ax+by+c=0 and the coordinate of P1 be (x0,y0). Then p1 has the equation (bx-ay)2-2Ax-2By+(a2+b2)(x02+y02)-c2=0, where A=(a2+b2)x0+ac and B=(a2+b2)y0+bc. Let the coordinate of P2 be (h,0), and p2 has the equation y2-2hx+h2=0, since the equation of L2 is x=0.
Let the crease be tangent to p1 at (x1,y1), and the crease has the equation (bC-A)x-(aC+B)y+Ax1+By1-C2=0, where C=bx1-ay1. Let the crease be tangent to p2 at (x2,y2), and the crease has the equation hx-y2y+h(x2-h)=0. Since these equations express the same line, we get three equations: kh=bC-A, ky2=aC+B, and kh(x2-h)=Ax1+By1-C2, where k is a nonzero constant.
When P2 comes close to L2, h approximates to 0. So do kh and kh(x2-h). At the limit, P2 gets onto L2. If kh=0, the equation of the crease is (aC+B)(y-y1)=0. That means the crease is a tangent of p1 perpendicular to the y-axis, namely L2. If kh(x2-h)=0, the equation of the crease is (bC-A)x-(aC+B)y=0. That means the crease is a tangent of p1 passing through the origin, namely P2.
Therefore, we can define a line placing point P onto line L when P is on L as either a line perpendicular to L or a line passing through P. Then, we can consider the fold E and G as the fold F with P2 being on L2. We can also consider the fold C and D as the fold F with P1 being on L1 and P2 being on L2 at the same time.
All things considered, we need only one fold in the origami construction. Therefore, we can define the origami construction as a finite sequence of the following two procedures on a plane with some lines placed arbitrarily.
1. Given some lines, to locate points of intersection.
2. Given two point P1 and P2 and two lines L1 and L2, to fold a line placing P1 onto L1 and placing P2 onto L2. (A line placing point P onto line L when P is on L is either a line perpendicular to L or a line passing through P.)
It is known that the straight-edge-and-compass construction is equivalent to solving quadratic equations. On the other hand, the origami construction is equivalent to solving cubic equations. So, any line or point can be constructed with origami if it can be constructed with a straight edge and a compass. In addition, we can solve with origami some problems which cannot be solved with a straight edge and a compass, such as doubling a cube or trisecting an angle.
Now, let's solve the cubic equation x3+ax2+bx+c=0 with origami. Let two points P1 and P2 have the coordinates (a,1) and (c,b), respectively. Also let two lines L1 and L2 have the equations y+1=0 and x+c=0, respectively. Fold a line placing P1 onto L1 and placing P2 onto L2, and the slope of the crease is the solution of x3+ax2+bx+c=0.
I will explain why. Let p1 be a parabola having the focus P1 and the directrix L1. Since the crease is not parallel to the y-axis, we can let the crease have the equation y=tx+u. Let the crease be tangent to p1 at (x1,y1), and (x1-a)2=4y1. Because the crease has the equation (x1-a)(x-x1)=2(y-y1), we get t=(x1-a)/2 and u=y1-x1(x1-a)/2. From these equations, we get u=-t2-at.
When c is not 0, let p2 be a parabola having the focus P2 and the directrix L2. Let the crease be tangent to p2 at (x2,y2), and (y2-b)2=4cx2. Because the crease has the equation (y2-b)(y-y2)=2c(x-x2), we get t=2c/(y2-b) and u=y2-2cx2/(y2-b). From these equations, we get u=b+c/t. (t is not 0 because the crease is not parallel to the x-axis.) Therefore, t3+at2+bt+c=0.
When c is 0, P2 is on L2. So, either the crease is perpendicular to L2 or the crease passes through P2. In the former case, t=0. In the later case, u=b, and t2+at+b=0. Therefore t3+at2+bt+c=0.
We can double a cube by solving the equation x3-2=0.
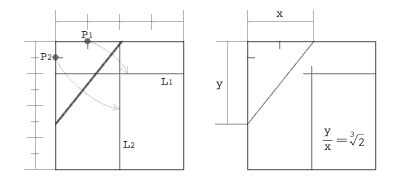
We can also trisect an angle by solving the equation x3+3tx2-3x-t=0, where t=1/tanθ and x=tan(θ/3-π/2).