数学の作図というと、定規とコンパスを使うのが普通です。定規とコンパスの作図とは、任意の位置にいくつかの点が置かれた平面の上で、以下の三つの操作を有限回くり返して作図することです。
1. 二つの点 P1 と P2 があるとき、P1 と P2 の両方を通る直線を描く。
2. 一つの点 O と、一本の線分 P1P2 があるとき、O を中心として、P1P2 の長さを半径とする円を描く。
3. 直線や円がいくつかあるとき、それらが交わるところに点を置く。
折り紙を使っても、いろいろな作図ができます。折り紙の作図では、もちろん「折る」という動作を使うのですが、ひとくちに「折る」といっても、いろいろな折り方があります。どういう折り方を使えばよいでしょうか。
まず、曲線に沿って折ったり、一度に複数の直線で折ったりするのは除外しましょう。このような折り方の数学的な解析は非常に難しいからです。一度に一本の直線を折るだけだとします。また、いっさいの道具は使ってはいけないとしましょう。物差しで測って印をつけるとか、紙を二枚以上使うとか、鉛筆で印をつけるのも禁止します。
そのように定めると、折り紙の作図では、平面の上にいきなり点を置くことはできません。平面を任意の位置で折ったとき、できるのは一本の直線です。点を置くには、その点を通る二本の直線を折るしかありません。逆にいえば、折り紙の作図では、平面の上に点があるとき、その点を通る直線が必ず二本以上存在しています。
そこで、折り紙の作図を定義するとしたら、任意の位置にいくつかの直線が置かれた平面の上で、「道具を使わず一度に一本の直線を折る」という動作と「折り目が交わるところに点を置く」という動作の有限回のくり返しだということになるでしょう。
折り紙の作図で使う折り方のリストとして、藤田文章は、以下の六つの折り方を挙げました。
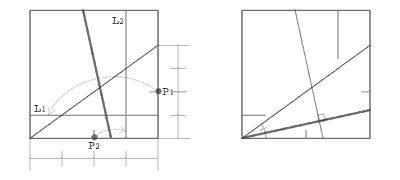
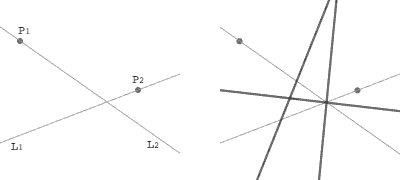
A. 二本の直線 L1 と L2 があるとき、L1 を L2 に合わせる直線を折る。
B. 二つの点 P1 と P2 があるとき、P1 を P2 に合わせる直線を折る。
C. 二つの点 P1 と P2 があるとき、P1 と P2 の両方を通る直線を折る。
D. 一つの点 P と一本の直線 L があるとき、P を通って L に垂直な直線を折る。
E. 二つの点 P1 と P2、一本の直線 L があるとき、P1 を L の上に乗せ、P2 を通る直線を折る。
F. 二つの点 P1 と P2、二本の直線 L1 と L2 があるとき、P1 を L1 の上に乗せ、P2 を L2 の上に乗せる直線を折る。
もう一つの折り方を、私が見つけました。
G. 一つの点 P、二本の直線 L1 と L2 があるとき、P を L1 の上に乗せ、L2 に垂直な直線を折る。
ロバート・ラングが、この七つの折り方が完全であることを証明しました。つまり、折り紙の作図で使う折り方はこれで全部です。すべての作図をするのに、七つより多い折り方は必要ありません。では、七つすべてが必要なのでしょうか。実は、折り方は一つだけで十分なのです。
まず、Aの折り方は、Fの折り方で、点 P1 が直線 L2 の上にあり、点 P2 が直線 L1 の上にある場合だと考えられます。二本の直線 L1 と L2 があるとき、もう一本任意の直線を使って、L1 の上に点 P2 を置き、L2 の上に点 P1 を置くことができます。
また、Bの折り方も、Fの折り方で、点 P1 が直線 L2 の上にあり、点 P2 が直線 L1 の上にある場合だと考えられます。折り紙の作図では、二つの点 P1 と P2 があるとき、P1 を通って P2 を通らない直線 L2 と、P2 を通って P1 を通らない直線 L1 が必ず存在しています。

さて、Fの折り方で折れる直線は、P1 を焦点として L1 を準線とする放物線 p1 と、P2 を焦点として L2 を準線とする放物線 p2 との共通接線になることが知られています。ここで、P2 を L2 に近づけていったときの極限として、P2 が L2 の上にある場合を考えます。
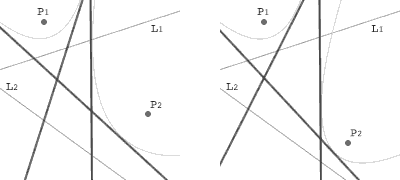
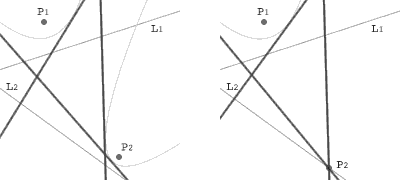
P2 がx軸の上にあって、L2 がy軸と重なるように、直交座標を設定します。このとき、L1 を表す方程式が ax+by+c=0 であり、P1 の座標が (x0,y0) となっているとします。p1 を表す方程式は、(a2+b2)x0+ac=A として、(a2+b2)y0+bc=B とすれば、(bx-ay)2-2Ax-2By+(a2+b2)(x02+y02)-c2=0 です。P2 の座標を (h,0) とすると、L2 を表す方程式は x=0 ですから、p2を表す方程式は y2-2hx+h2=0 です。
折り目と p1 との接点の座標を (x1,y1) とすると、折り目を表す方程式は、bx1-ay1=C として、(bC-A)x-(aC+B)y+Ax1+By1-C2=0 と表せます。また、折り目と p2 との接点の座標を (x2,y2) とすると、折り目を表す方程式は hx-y2y+h(x2-h)=0 と表せます。この二つの方程式は同じ直線を表していますから、0でない定数を k として、kh=bC-A、ky2=aC+B、kh(x2-h)=Ax1+By1-C2 の三つの方程式が成り立ちます。
ここで、P2 を L2 に近づけていくと、h が0に近づきますから、kh と kh(x2-h) が0に近づきます。P2 が L2 の上に乗ったとき、kh=0 とすると、折り目は (aC+B)(y-y1)=0 という方程式で表されます。これは、p1 の接線のうち、y軸に垂直なもの、すなわち L2 に垂直なものにほかなりません。また、kh(x2-h)=0 とすると、折り目は (bC-A)x-(aC+B)y=0 という方程式で表されます。これは、p1 の接線のうち、原点を通るもの、すなわち P2 を通るものにほかなりません。
そこで、点 P が直線 L の上にあるとき、P を L の上に乗せる直線とは、L に垂直な直線か、または P を通る直線だと定義します。すると、Eの折り方とGの折り方は、Fの折り方で、P2 が L2 の上にある場合だと考えられます。また、Cの折り方とDの折り方も、Fの折り方で、P1 が L1 の上にあり、同時に P2 が L2 の上にある場合だと考えられます。
結局、折り紙の作図では、折り方は一つだけあればいいということがわかりました。ですから、折り紙の作図とは、任意の位置にいくつかの直線が置かれた平面の上で、以下の二つの操作を有限回くり返して作図することです。
1. 直線がいくつかあるとき、それらが交わるところに点を置く。
2. 二つの点 P1 と P2、二本の直線 L1 と L2 があるとき、P1 を L1 の上に乗せ、P2 を L2 の上に乗せる直線を折る。(ただし、点 P が直線 L の上にあるとき、P を L の上に乗せる直線とは、L に垂直な直線か、または P を通る直線である。)
定規とコンパスを使った作図は、本質的には二次方程式を解くことと同じであることが知られています。一方、折り紙を使った作図は、本質的には三次方程式を解くことと同じです。ですから、定規とコンパスで作図できる点と直線は全て、折り紙でも作図できます。また、定規とコンパスの作図では解くことのできない、立方体倍積問題や角の三等分問題などが、折り紙の作図で解けます。
x3+ax2+bx+c=0 という三次方程式の解は、折り紙の作図を使って、次のように求められます。xy平面上で、(a,1) という座標にある点を P1 として、(c,b) という座標にある点を P2 とします。また、y+1=0 という方程式であらわされる直線を L1 として、x+c=0 という方程式であらわされる直線を L2 とします。ここで、P1 を L1 の上に乗せ、P2 を L2 の上に乗せる直線を折ると、折り目の傾きが x3+ax2+bx+c=0 の解になります。
どうしてそうなるのか、説明しましょう。点 P1 を焦点として直線 L1 を準線とする放物線を p1 とします。折り目がy軸と平行になることはありませんので、折り目を表す方程式を y=tx+u とおきます。折り目が p1 と点 (x1,y1) で接するとすると、(x1-a)2=4y1 が成り立ちます。また、折り目の方程式は (x1-a)(x-x1)=2(y-y1) と書けますから、t=(x1-a)/2、u=y1-x1(x1-a)/2 が成り立ちます。これらの式から、u=-t2-at となります。
c が0でないとき、点 P2 を焦点として直線 L2 を準線とする放物線を p2 とします。折り目が p2 と点 (x2,y2) で接するとすると、(y2-b)2=4cx2 が成り立ちます。また、折り目の方程式は (y2-b)(y-y2)=2c(x-x2) と書けますから、t=2c/(y2-b)、u=y2-2cx2/(y2-b) が成り立ちます。これらの式から、u=b+c/t となります。(折り目がx軸と平行になることもないので、t は0ではありません。)したがって、t3+at2+bt+c=0 が成り立ちます。
c が0のとき、P2 は L2 の上にあるので、折り目は L2 に垂直か P2 を通るかどちらかです。前者の場合 t=0 です。後者の場合、u=b ですから、t2+at+b=0 です。したがって、t3+at2+bt+c=0 が成り立ちます。
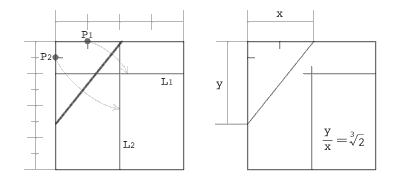
この三次方程式の解法を使って、立方体倍積問題を解くには、x3-2=0 という方程式を解きます。
また、角の三等分問題を解くには、t=1/tanθ として、x=tan(θ/3-π/2) とすると、x3+3tx2-3x-t=0 という方程式が成り立ちますから、これを利用すると、簡単に作図できます。